House Prices - Advanced Regression Techniques (Python)#
Predict sales prices and practice feature engineering, RFs, and gradient boosting
Author: Lingsong Zeng
Date: 12/31/2024
Introduction#
Overview#
This competition runs indefinitely with a rolling leaderboard. Learn more
Description#

Ask a home buyer to describe their dream house, and they probably won’t begin with the height of the basement ceiling or the proximity to an east-west railroad. But this playground competition’s dataset proves that much more influences price negotiations than the number of bedrooms or a white-picket fence.
With 79 explanatory variables describing (almost) every aspect of residential homes in Ames, Iowa, this competition challenges you to predict the final price of each home.
Practice Skills#
Creative feature engineering
Advanced regression techniques like random forest and gradient boosting
Acknowledgments#
The Ames Housing dataset was compiled by Dean De Cock for use in data science education. It’s an incredible alternative for data scientists looking for a modernized and expanded version of the often cited Boston Housing dataset.
Photo by Tom Thain on Unsplash.
Evaluation#
Goal#
It is my job to predict the sales price for each house. For each Id in the test set, predict the value of the SalePrice variable.
Metric#
Submissions are evaluated on Root-Mean-Squared-Error (RMSE) between the logarithm of the predicted value and the logarithm of the observed sales price. (Taking logs means that errors in predicting expensive houses and cheap houses will affect the result equally.)
# Import required libraries
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import root_mean_squared_error
from sklearn.experimental import enable_iterative_imputer # noqa
from sklearn.impute import IterativeImputer
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import RepeatedKFold, GridSearchCV, RandomizedSearchCV
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
from sklearn.tree import DecisionTreeRegressor
from xgboost import XGBRegressor, DMatrix
from lightgbm import LGBMRegressor
from sklearn.ensemble import RandomForestRegressor, BaggingRegressor, StackingRegressor
Data#
File descriptions#
train.csv- the training settest.csv- the test setdata_description.txt- full description of each column, originally prepared by Dean De Cock but lightly edited to match the column names used heresample_submission.csv- a benchmark submission from a linear regression on year and month of sale, lot square footage, and number of bedrooms
# Define paths for train and test datasets
train_path = os.path.join('data', 'house-prices', 'raw', 'train.csv')
test_path = os.path.join('data', 'house-prices', 'raw', 'test.csv')
# Load datasets
train = pd.read_csv(train_path)
test = pd.read_csv(test_path)
Here we using os.path.join , the dynamic path generation, instead of using hard-coded paths is aiming to provide better compatibility across different platforms.
Different operating systems use different path separators (e.g. Windows uses \, while Linux and macOS use /). os.path.join automatically chooses the correct separator based on the operating system.
# Basic dataset overview
print("Train dataset shape:", train.shape)
print("Test dataset shape:", test.shape)
Train dataset shape: (1460, 81)
Test dataset shape: (1459, 80)
The size of the training dataset and the test dataset are roughly the same. The test dataset has one less column than the training dataset, which is our target column SalePrice.
train.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1460 entries, 0 to 1459
Data columns (total 81 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Id 1460 non-null int64
1 MSSubClass 1460 non-null int64
2 MSZoning 1460 non-null object
3 LotFrontage 1201 non-null float64
4 LotArea 1460 non-null int64
5 Street 1460 non-null object
6 Alley 91 non-null object
7 LotShape 1460 non-null object
8 LandContour 1460 non-null object
9 Utilities 1460 non-null object
10 LotConfig 1460 non-null object
11 LandSlope 1460 non-null object
12 Neighborhood 1460 non-null object
13 Condition1 1460 non-null object
14 Condition2 1460 non-null object
15 BldgType 1460 non-null object
16 HouseStyle 1460 non-null object
17 OverallQual 1460 non-null int64
18 OverallCond 1460 non-null int64
19 YearBuilt 1460 non-null int64
20 YearRemodAdd 1460 non-null int64
21 RoofStyle 1460 non-null object
22 RoofMatl 1460 non-null object
23 Exterior1st 1460 non-null object
24 Exterior2nd 1460 non-null object
25 MasVnrType 588 non-null object
26 MasVnrArea 1452 non-null float64
27 ExterQual 1460 non-null object
28 ExterCond 1460 non-null object
29 Foundation 1460 non-null object
30 BsmtQual 1423 non-null object
31 BsmtCond 1423 non-null object
32 BsmtExposure 1422 non-null object
33 BsmtFinType1 1423 non-null object
34 BsmtFinSF1 1460 non-null int64
35 BsmtFinType2 1422 non-null object
36 BsmtFinSF2 1460 non-null int64
37 BsmtUnfSF 1460 non-null int64
38 TotalBsmtSF 1460 non-null int64
39 Heating 1460 non-null object
40 HeatingQC 1460 non-null object
41 CentralAir 1460 non-null object
42 Electrical 1459 non-null object
43 1stFlrSF 1460 non-null int64
44 2ndFlrSF 1460 non-null int64
45 LowQualFinSF 1460 non-null int64
46 GrLivArea 1460 non-null int64
47 BsmtFullBath 1460 non-null int64
48 BsmtHalfBath 1460 non-null int64
49 FullBath 1460 non-null int64
50 HalfBath 1460 non-null int64
51 BedroomAbvGr 1460 non-null int64
52 KitchenAbvGr 1460 non-null int64
53 KitchenQual 1460 non-null object
54 TotRmsAbvGrd 1460 non-null int64
55 Functional 1460 non-null object
56 Fireplaces 1460 non-null int64
57 FireplaceQu 770 non-null object
58 GarageType 1379 non-null object
59 GarageYrBlt 1379 non-null float64
60 GarageFinish 1379 non-null object
61 GarageCars 1460 non-null int64
62 GarageArea 1460 non-null int64
63 GarageQual 1379 non-null object
64 GarageCond 1379 non-null object
65 PavedDrive 1460 non-null object
66 WoodDeckSF 1460 non-null int64
67 OpenPorchSF 1460 non-null int64
68 EnclosedPorch 1460 non-null int64
69 3SsnPorch 1460 non-null int64
70 ScreenPorch 1460 non-null int64
71 PoolArea 1460 non-null int64
72 PoolQC 7 non-null object
73 Fence 281 non-null object
74 MiscFeature 54 non-null object
75 MiscVal 1460 non-null int64
76 MoSold 1460 non-null int64
77 YrSold 1460 non-null int64
78 SaleType 1460 non-null object
79 SaleCondition 1460 non-null object
80 SalePrice 1460 non-null int64
dtypes: float64(3), int64(35), object(43)
memory usage: 924.0+ KB
categorical_features = [
'MSSubClass', 'MSZoning', 'Street', 'Alley', 'LotShape', 'LandContour',
'Utilities', 'LotConfig', 'LandSlope', 'Neighborhood', 'Condition1',
'Condition2', 'BldgType', 'HouseStyle', 'RoofStyle', 'RoofMatl',
'Exterior1st', 'Exterior2nd', 'MasVnrType', 'ExterQual', 'ExterCond',
'Foundation', 'BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1',
'BsmtFinType2', 'Heating', 'HeatingQC', 'CentralAir', 'Electrical',
'KitchenQual', 'Functional', 'FireplaceQu', 'GarageType', 'GarageFinish',
'GarageQual', 'GarageCond', 'PavedDrive', 'PoolQC', 'Fence', 'MiscFeature',
'SaleType', 'SaleCondition', 'OverallQual', 'OverallCond'
]
numerical_features = [
'LotFrontage', 'LotArea', 'YearBuilt', 'YearRemodAdd', 'MasVnrArea',
'BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', '1stFlrSF',
'2ndFlrSF', 'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath',
'FullBath', 'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'TotRmsAbvGrd',
'Fireplaces', 'GarageYrBlt', 'GarageCars', 'GarageArea', 'WoodDeckSF',
'OpenPorchSF', 'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea',
'MiscVal', 'MoSold', 'YrSold'
]
For categorical_features and numerical_features, the reason we cannot directly select features with values of int64 or float64, because some features such as MSSubClass:
MSSubClass: Identifies the type of dwelling involved in the sale.
20 1-STORY 1946 & NEWER ALL STYLES
30 1-STORY 1945 & OLDER
40 1-STORY W/FINISHED ATTIC ALL AGES
45 1-1/2 STORY - UNFINISHED ALL AGES
50 1-1/2 STORY FINISHED ALL AGES
60 2-STORY 1946 & NEWER
70 2-STORY 1945 & OLDER
75 2-1/2 STORY ALL AGES
80 SPLIT OR MULTI-LEVEL
85 SPLIT FOYER
90 DUPLEX - ALL STYLES AND AGES
120 1-STORY PUD (Planned Unit Development) - 1946 & NEWER
150 1-1/2 STORY PUD - ALL AGES
160 2-STORY PUD - 1946 & NEWER
180 PUD - MULTILEVEL - INCL SPLIT LEV/FOYER
190 2 FAMILY CONVERSION - ALL STYLES AND AGES
Its value is int64 format, but it is actually a categorical feature. Therefore, here I manually distinguish all categorical_features and numerical_features according to the description in data_description.txt.
none_features = {
'Alley': 'NoAlley',
'BsmtQual': 'NoBsmt',
'BsmtCond': 'NoBsmt',
'BsmtExposure': 'NoBsmt',
'BsmtFinType1': 'NoBsmt',
'BsmtFinType2': 'NoBsmt',
'FireplaceQu': 'NoFireplace',
'GarageType': 'NoGarage',
'GarageFinish': 'NoGarage',
'GarageQual': 'NoGarage',
'GarageCond': 'NoGarage',
'PoolQC': 'NoPool',
'Fence': 'NoFence',
'MiscFeature': 'NoFeature'
}
According to the description in data_description.txt, NA in some features does not mean Missing Value, but means that the observation does not have the feature, such as Alley:
Alley: Type of alley access to property
Grvl Gravel
Pave Paved
NA No alley access
Therefore, the missing value filling treatment of these features should be different. I filtered out all similar features here to prepare for the missing value filling in the subsequent preprocessing.
for feature, value in none_features.items():
train[feature] = train[feature].fillna(value)
test[feature] = test[feature].fillna(value)
ordinal_features = [
"MSSubClass", "OverallQual", "OverallCond", "LotShape", "LandSlope",
"ExterQual", "ExterCond", "BsmtQual", "BsmtCond", "BsmtExposure",
"BsmtFinType1", "BsmtFinType2", "HeatingQC", "KitchenQual",
"Functional", "FireplaceQu", "GarageFinish", "GarageQual", "GarageCond",
"PavedDrive", "PoolQC", "Fence"
]
nominal_features = [
"MSZoning", "Street", "Alley", "LandContour", "Utilities", "LotConfig",
"Neighborhood", "Condition1", "Condition2", "BldgType", "HouseStyle",
"RoofStyle", "RoofMatl", "Exterior1st", "Exterior2nd", "MasVnrType",
"Foundation", "Heating", "CentralAir", "Electrical", "GarageType",
"MiscFeature", "SaleType", "SaleCondition"
]
Similarly, I also distinguish between ordinal_features and nominal_features here to facilitate subsequent preprocessing. The main difference between them is whether the variable values are ordered. The following are examples of an ordinal feature and a nominal feature respectively.
ExterQual: Evaluates the quality of the material on the exterior
Ex Excellent
Gd Good
TA Average/Typical
Fa Fair
Po Poor
MSZoning: Identifies the general zoning classification of the sale.
A Agriculture
C Commercial
FV Floating Village Residential
I Industrial
RH Residential High Density
RL Residential Low Density
RP Residential Low Density Park
RM Residential Medium Density
In the following preprocessing, ordinal features will be applied with Label Encoding, while nominal features will be applied with One-Hot Encoding.
EDA#
# Summary statistics for SalePrice
print(train['SalePrice'].describe())
count 1460.000000
mean 180921.195890
std 79442.502883
min 34900.000000
25% 129975.000000
50% 163000.000000
75% 214000.000000
max 755000.000000
Name: SalePrice, dtype: float64
# Plot the distribution of SalePrice
sns.histplot(train['SalePrice'], bins=20, kde=True)
plt.title('SalePrice Distribution')
plt.show()
# Check skewness and kurtosis of SalePrice
print("Skewness of SalePrice:", train['SalePrice'].skew())
print("Kurtosis of SalePrice:", train['SalePrice'].kurt())
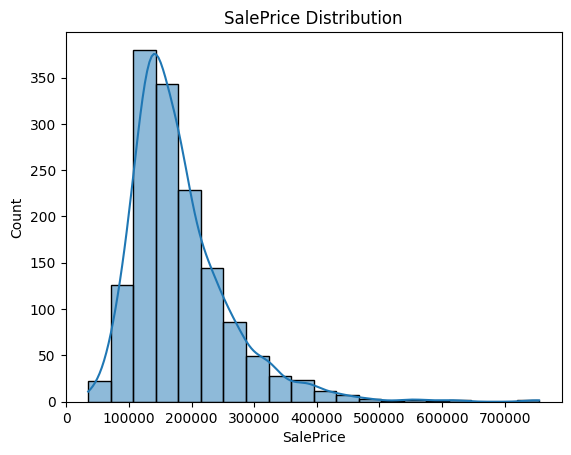
Skewness of SalePrice: 1.8828757597682129
Kurtosis of SalePrice: 6.536281860064529
From the histogram and the calculated value of skewness (1.88), we can see that the distribution of SalePrice is right-skewed. This may have a negative impact on the training of the model. So we need a log transformation for SalePrice.
train['LogSalePrice'] = np.log1p(train['SalePrice'])
We use np.log1p() instead of np.log() to handle zero values, since log(0) does not exist. np.log1p() is a shorthand for log(x+1) and ensures that the target value is non-negative.
sns.histplot(train['LogSalePrice'], bins=20, kde=True)
plt.title("Log-Transformed SalePrice Distribution")
plt.show()
print("Skewness of (Log-Transformed) SalePrice:", train['LogSalePrice'].skew())
print("Kurtosis of (Log-Transformed) SalePrice:", train['LogSalePrice'].kurt())
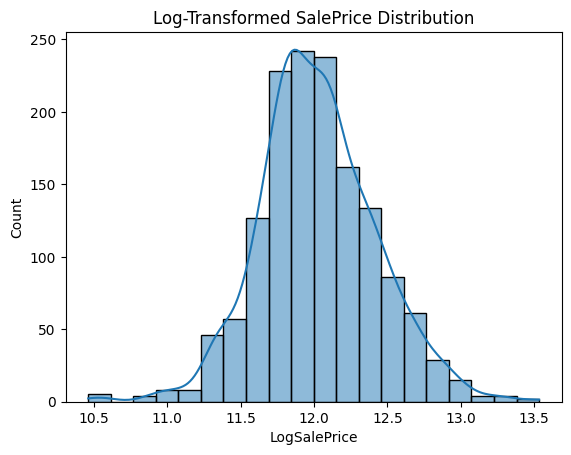
Skewness of (Log-Transformed) SalePrice: 0.12134661989685333
Kurtosis of (Log-Transformed) SalePrice: 0.809519155707878
From the charts and statistics, we can see that after logarithmic transformation, the distribution of SalePrice is closer to normal distribution.
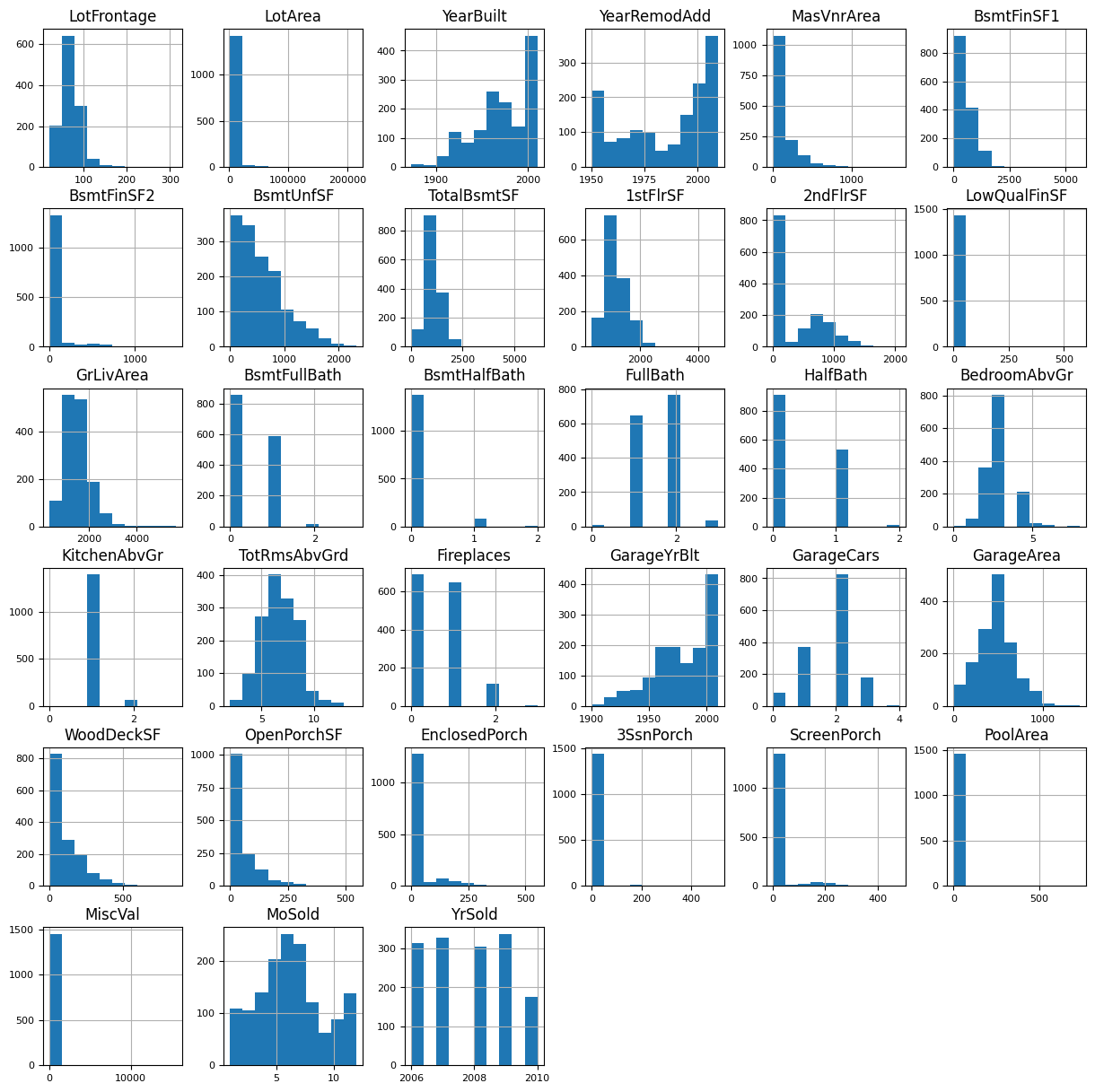
The following is the distribution of the remaining numerical features:
train[numerical_features].hist(figsize=(15, 15), bins=10, xlabelsize=8, ylabelsize=8);
Feature Engineering#
def add_features(data, create_interactions=True, create_base_features=True):
"""
Add new features to the dataset.
Parameters:
- data: DataFrame, the input data.
- create_interactions: bool, whether to create interaction and polynomial features.
- create_base_features: bool, whether to create base features like `HouseAge`.
Returns:
- DataFrame with new features added.
"""
# Create a DataFrame to store new features
new_features = pd.DataFrame(index=data.index)
# Base features
if create_base_features:
new_features['HouseAge'] = data['YrSold'] - data['YearBuilt']
new_features['RemodelAge'] = data['YrSold'] - data['YearRemodAdd']
new_features['TotalSF'] = data['1stFlrSF'] + data['2ndFlrSF'] + data['TotalBsmtSF']
# Interaction and polynomial features
if create_interactions:
new_features['GrLivArea_OverallQual'] = data['GrLivArea'] * data['OverallQual']
new_features['GrLivArea^2'] = data['GrLivArea'] ** 2
new_features['OverallQual^2'] = data['OverallQual'] ** 2
# Add the new features to the original dataset
data = pd.concat([data, new_features], axis=1)
return data
train = add_features(train)
test = add_features(test)
new_features = [
'HouseAge', 'RemodelAge', 'TotalSF',
'GrLivArea_OverallQual', 'GrLivArea^2', 'OverallQual^2'
]
numerical_features.extend(new_features)
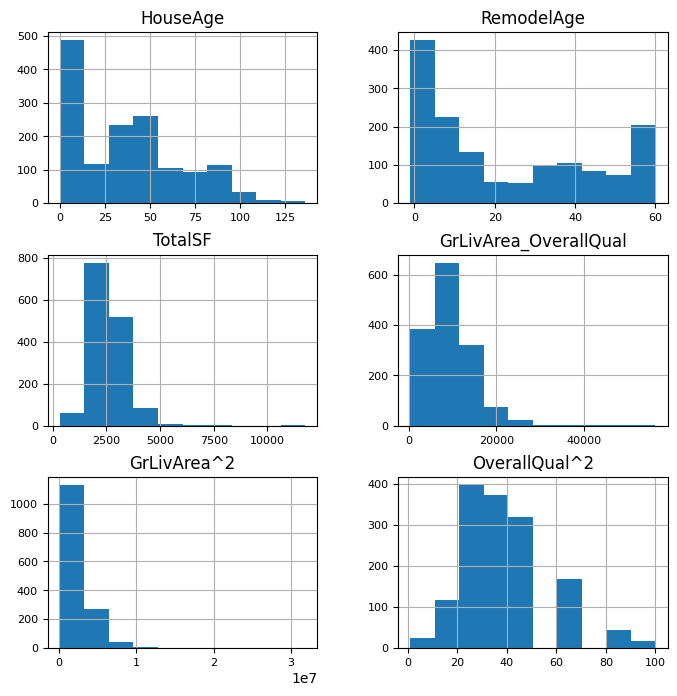
train[new_features].hist(figsize=(8, 8), bins=10, xlabelsize=8, ylabelsize=8);
Preprocessing#
test_ids = test['Id']
X_train = train.drop(columns=['Id', 'SalePrice', 'LogSalePrice'])
y_train = train['LogSalePrice']
X_test = test.drop(columns=['Id'])
Here we drop the extra columns and set the log transformed SalePrice as y. We also save the Id of the test set, which will be used when submitting to Kaggle later. (The standard submission format is shown in sample_submission.csv)
ordinal_mappings = {
"MSSubClass": {
20: 1, 30: 2, 40: 3, 45: 4, 50: 5,
60: 6, 70: 7, 75: 8, 80: 9, 85: 10,
90: 11, 120: 12, 150: 13, 160: 14,
180: 15, 190: 16
},
"LotShape": {"Reg": 3, "IR1": 2, "IR2": 1, "IR3": 0},
"LandSlope": {"Gtl": 2, "Mod": 1, "Sev": 0},
"ExterQual": {"Ex": 4, "Gd": 3, "TA": 2, "Fa": 1, "Po": 0},
"ExterCond": {"Ex": 4, "Gd": 3, "TA": 2, "Fa": 1, "Po": 0},
"BsmtQual": {"Ex": 5, "Gd": 4, "TA": 3, "Fa": 2, "Po": 1, "NoBsmt": 0},
"BsmtCond": {"Ex": 5, "Gd": 4, "TA": 3, "Fa": 2, "Po": 1, "NoBsmt": 0},
"BsmtExposure": {"Gd": 4, "Av": 3, "Mn": 2, "No": 1, "NoBsmt": 0},
"BsmtFinType1": {"GLQ": 6, "ALQ": 5, "BLQ": 4, "Rec": 3, "LwQ": 2, "Unf": 1, "NoBsmt": 0},
"BsmtFinType2": {"GLQ": 6, "ALQ": 5, "BLQ": 4, "Rec": 3, "LwQ": 2, "Unf": 1, "NoBsmt": 0},
"HeatingQC": {"Ex": 4, "Gd": 3, "TA": 2, "Fa": 1, "Po": 0},
"KitchenQual": {"Ex": 4, "Gd": 3, "TA": 2, "Fa": 1, "Po": 0},
"Functional": {
"Typ": 7, "Min1": 6, "Min2": 5, "Mod": 4,
"Maj1": 3, "Maj2": 2, "Sev": 1, "Sal": 0
},
"FireplaceQu": {"Ex": 5, "Gd": 4, "TA": 3, "Fa": 2, "Po": 1, "NoFireplace": 0},
"GarageFinish": {"Fin": 3, "RFn": 2, "Unf": 1, "NoGarage": 0},
"GarageQual": {"Ex": 5, "Gd": 4, "TA": 3, "Fa": 2, "Po": 1, "NoGarage": 0},
"GarageCond": {"Ex": 5, "Gd": 4, "TA": 3, "Fa": 2, "Po": 1, "NoGarage": 0},
"PavedDrive": {"Y": 2, "P": 1, "N": 0},
"PoolQC": {"Ex": 4, "Gd": 3, "TA": 2, "Fa": 1, "NoPool": 0},
"Fence": {"GdPrv": 4, "MnPrv": 3, "GdWo": 2, "MnWw": 1, "NoFence": 0},
"MiscFeature": {"Gar2": 4, "Shed": 3, "TenC": 2, "Othr": 1, "NoFeature": 0},
"Alley": {"Grvl": 2, "Pave": 1, "NoAlley": 0},
"OverallQual": {i: i for i in range(1, 11)}, # 1-10
"OverallCond": {i: i for i in range(1, 11)} # 1-10
}
LabelEncoder may encode Ex as 0 and Po as 4, which completely reverses the actual meaning. This is due to LabelEncoder assigns values in alphabetical order of categories, which can lead to incorrect assumptions about the order (e.g., A > B > C). Hence, in order to avoid this, we created this ordinal_mappings.
for feature in categorical_features:
# assign type as category
X_train[feature] = X_train[feature].astype("category")
X_test[feature] = X_test[feature].astype("category")
# label encoding
if feature in ordinal_mappings:
X_train[feature] = X_train[feature].map(ordinal_mappings[feature])
X_test[feature] = X_test[feature].map(ordinal_mappings[feature])
original_columns = set(X_train.columns)
# one-hot encoding
X_train = pd.get_dummies(X_train, columns=nominal_features, dummy_na=True)
X_test = pd.get_dummies(X_test, columns=nominal_features, dummy_na=True)
# align train and test
X_train, X_test = X_train.align(X_test, join='outer', axis=1)
new_columns = list(set(X_train.columns) - original_columns)
# Fill missing values with 0
X_train[new_columns] = X_train[new_columns].fillna(0)
X_test[new_columns] = X_test[new_columns].fillna(0)
# Define the Iterative Imputer with Random Forest Regressor
iter_imputer = IterativeImputer(
estimator=RandomForestRegressor(
n_estimators=100, # Number of trees
n_jobs=-1, # Use all available cores
random_state=42
),
max_iter=10,
random_state=42
)
# Fit and transform the train and test
X_train_full = iter_imputer.fit_transform(X_train)
X_test_full = iter_imputer.transform(X_test)
X_train_full = pd.DataFrame(X_train_full, columns=X_train.columns, index=X_train.index)
X_test_full = pd.DataFrame(X_test_full, columns=X_test.columns, index=X_test.index)
scaler = StandardScaler()
X_train_full[numerical_features] = scaler.fit_transform(X_train_full[numerical_features])
X_test_full[numerical_features] = scaler.transform(X_test_full[numerical_features])
Split training data for single validation, RepeatedKFold can better evaluate the stability of the model than train_test_split, especially for small datasets.
rkf = RepeatedKFold(n_splits=5, n_repeats=10, random_state=42)
for train_idx, valid_idx in rkf.split(X_train_full, y_train):
X_train_split, X_valid_split = X_train_full.iloc[train_idx], X_train_full.iloc[valid_idx]
y_train_split, y_valid_split = y_train.iloc[train_idx], y_train.iloc[valid_idx]
break # Only return the first split for simplicity
Modeling#
def save_submission(model, X_test, test_ids, filename='submission.csv'):
"""
Generate predictions using the provided model and save them to a CSV file.
Parameters:
- model: Trained model that implements the `predict` method.
- X_test: ndarray or DataFrame, the test dataset containing the features.
- test_ids: array-like, unique identifiers for the test samples.
- filename: str, name of the output submission file. Default is 'submission.csv'.
The function predicts the target variable on the test set, applies an exponential
transformation to reverse log-transformation (if applied during training), and saves
the predictions along with the test IDs to a CSV file.
"""
predictions = np.expm1(model.predict(X_test)) # inverse log-transform
output_path = os.path.join('data', 'house-prices', 'processed(py)', filename)
submission = pd.DataFrame({
'Id': test_ids,
'SalePrice': predictions
})
submission.to_csv(output_path, index=False)
print(f"Submission file saved to: {output_path}")
kNN#
def train_knn(X_train, y_train):
# Define the kNN model
knn = KNeighborsRegressor()
# Set up hyperparameter grid for tuning
param_grid = {
'n_neighbors': range(1, 11), # 1-10
'weights': ['uniform', 'distance'],
'p': [1, 2] # Manhattan distance (p=1)
} # Euclidean distance (p=2)
# Use GridSearchCV to find the best hyperparameters
grid_search = GridSearchCV(
estimator=knn,
param_grid=param_grid,
scoring='neg_root_mean_squared_error',
cv=5, # 5-fold cross-validation
verbose=1,
n_jobs=-1 # Use all available cores
)
# Fit the grid search to the training data
grid_search.fit(X_train, y_train)
# Print the best parameters and RMSE
print("Best parameters:", grid_search.best_params_)
print("Best RMSE:", -grid_search.best_score_)
# Use the best model to predict on the test set
return grid_search.best_estimator_
knn_model = train_knn(X_train_split, y_train_split)
Fitting 5 folds for each of 40 candidates, totalling 200 fits
Best parameters: {'n_neighbors': 8, 'p': 1, 'weights': 'distance'}
Best RMSE: 0.15161816222293886
knn_valid_pred = knn_model.predict(X_valid_split)
knn_valid_rmse = root_mean_squared_error(y_valid_split, knn_valid_pred)
print(f"Validation RMSE (kNN): {knn_valid_rmse}")
Validation RMSE (kNN): 0.17032522997840102
save_submission(knn_model, X_test_full, test_ids, 'knn.csv')
Submission file saved to: data\house-prices\processed(py)\knn.csv
SVM#
def train_svm(X_train, y_train):
# Define the SVM model
svm_model = SVR()
# Set up hyperparameter grid for tuning
param_grid = {
'C': [0.1, 1, 10], # Regularization strength
'epsilon': [0.01, 0.1], # Epsilon-insensitive loss
'kernel': ['linear', 'rbf'], # Kernel types
'gamma': ['scale', 'auto']
}
# Use GridSearchCV to find the best hyperparameters
grid_search = GridSearchCV(
estimator=svm_model,
param_grid=param_grid,
scoring='neg_root_mean_squared_error', # minimize RMSE
cv=5, # 5-fold cross-validation
verbose=1,
n_jobs=-1 # use all available cores
)
# Fit the grid search to the training data
grid_search.fit(X_train, y_train)
# Print the best parameters and RMSE
print("Best parameters:", grid_search.best_params_)
print("Best RMSE:", -grid_search.best_score_)
# Use the best model to predict on the test set
return grid_search.best_estimator_
svm_model = train_svm(X_train_split, y_train_split)
Fitting 5 folds for each of 24 candidates, totalling 120 fits
Best parameters: {'C': 1, 'epsilon': 0.01, 'gamma': 'scale', 'kernel': 'rbf'}
Best RMSE: 0.11875760276477298
svm_valid_pred = svm_model.predict(X_valid_split)
svm_valid_rmse = root_mean_squared_error(y_valid_split, svm_valid_pred)
print(f"Validation RMSE (SVM): {svm_valid_rmse}")
Validation RMSE (SVM): 0.12985131122581856
save_submission(svm_model, X_test_full, test_ids, 'svm.csv')
Submission file saved to: data\house-prices\processed(py)\svm.csv
Linear Regression#
linear_model = LinearRegression()
linear_model.fit(X_train_split, y_train_split)
linear_valid_pred = linear_model.predict(X_valid_split)
linear_valid_rmse = root_mean_squared_error(y_valid_split, linear_valid_pred)
print(f"Validation RMSE (Linear Regression): {linear_valid_rmse}")
Validation RMSE (Linear Regression): 108051429.92181346
save_submission(linear_model, X_test_full, test_ids, 'linear_regression.csv')
Submission file saved to: data\house-prices\processed(py)\linear_regression.csv
C:\Users\ArnoZ\AppData\Local\Temp\ipykernel_30220\1089569966.py:15: RuntimeWarning: overflow encountered in expm1
predictions = np.expm1(model.predict(X_test)) # inverse log-transform
Lasso#
def train_lasso(X_train, y_train):
# Define the Lasso model
lasso = Lasso(max_iter=10000, random_state=42, warm_start=True)
# Set up hyperparameter grid for tuning
param_grid = {
# More fine-grained alpha values for better regularization strength tuning
'alpha': np.logspace(-4, 2, 30) # From 0.0001 to 100, 30 evenly spaced values
}
# Use GridSearchCV to find the best hyperparameters
grid_search = GridSearchCV(
estimator=lasso,
param_grid=param_grid,
scoring='neg_root_mean_squared_error', # Minimize RMSE
cv=5, # 5-fold cross-validation
verbose=1,
n_jobs=-1 # Use all available cores
)
# Fit the grid search to the training data
grid_search.fit(X_train, y_train)
# Print the best parameters and RMSE
print("Best parameters (Lasso):", grid_search.best_params_)
print("Best RMSE (Lasso):", -grid_search.best_score_)
# Return the best Ridge model
return grid_search.best_estimator_
lasso_model = train_lasso(X_train_split, y_train_split)
Fitting 5 folds for each of 30 candidates, totalling 150 fits
Best parameters (Lasso): {'alpha': np.float64(0.0006723357536499335)}
Best RMSE (Lasso): 0.12663467044628274
lasso_valid_pred = lasso_model.predict(X_valid_split)
lasso_valid_rmse = root_mean_squared_error(y_valid_split, lasso_valid_pred)
print(f"Validation RMSE (Lasso): {lasso_valid_rmse}")
Validation RMSE (Lasso): 0.1338938110142784
save_submission(lasso_model, X_test_full, test_ids, 'lasso.csv')
Submission file saved to: data\house-prices\processed(py)\lasso.csv
Ridge#
def train_ridge(X_train, y_train):
# Define the Ridge model
ridge = Ridge(max_iter=10000, random_state=42)
# Set up hyperparameter grid for tuning
param_grid = {
'alpha': np.logspace(-3, 3, 13) # from 0.001 to 1000
}
# Use GridSearchCV to find the best hyperparameters
grid_search = GridSearchCV(
estimator=ridge,
param_grid=param_grid,
scoring='neg_root_mean_squared_error', # minimize RMSE
cv=5, # 5-fold cross-validation
verbose=1,
n_jobs=-1 # Use all available cores
)
# Fit the grid search to the training data
grid_search.fit(X_train, y_train)
# Print the best parameters and RMSE
print("Best parameters:", grid_search.best_params_)
print("Best RMSE:", -grid_search.best_score_)
# Return the best Ridge model
return grid_search.best_estimator_
ridge_model = train_ridge(X_train_split, y_train_split)
Fitting 5 folds for each of 13 candidates, totalling 65 fits
Best parameters: {'alpha': np.float64(3.1622776601683795)}
Best RMSE: 0.1278182559275935
ridge_valid_pred = ridge_model.predict(X_valid_split)
ridge_valid_rmse = root_mean_squared_error(y_valid_split, ridge_valid_pred)
print(f"Validation RMSE (Ridge): {ridge_valid_rmse}")
Validation RMSE (Ridge): 0.12965845670827755
save_submission(ridge_model, X_test_full, test_ids, 'ridge.csv')
Submission file saved to: data\house-prices\processed(py)\ridge.csv
ElasticNet#
def train_elasticnet(X_train, y_train):
# Define the ElasticNet model
elasticnet = ElasticNet(max_iter=10000, random_state=42)
# Set up hyperparameter grid for tuning
param_grid = {
'alpha': np.logspace(-4, 2, 13), # from 0.0001 to 100
'l1_ratio': np.linspace(0.1, 1.0, 10) # balance between L1 and L2 penalties
}
# Use GridSearchCV to find the best hyperparameters
grid_search = GridSearchCV(
estimator=elasticnet,
param_grid=param_grid,
scoring='neg_root_mean_squared_error', # minimize RMSE
cv=5, # 5-fold cross-validation
verbose=1,
n_jobs=-1 # Use all available cores
)
# Fit the grid search to the training data
grid_search.fit(X_train, y_train)
# Print the best parameters and RMSE
print("Best parameters:", grid_search.best_params_)
print("Best RMSE:", -grid_search.best_score_)
# Return the best ElasticNet model
return grid_search.best_estimator_
elasticnet_model = train_elasticnet(X_train_split, y_train_split)
Fitting 5 folds for each of 130 candidates, totalling 650 fits
Best parameters: {'alpha': np.float64(0.001), 'l1_ratio': np.float64(0.4)}
Best RMSE: 0.12578716262255227
elasticnet_valid_pred = elasticnet_model.predict(X_valid_split)
elasticnet_valid_rmse = root_mean_squared_error(y_valid_split, elasticnet_valid_pred)
print(f"Validation RMSE (Ridge): {elasticnet_valid_rmse}")
Validation RMSE (Ridge): 0.12972983276620062
save_submission(elasticnet_model, X_test_full, test_ids, 'elasticnet.csv')
Submission file saved to: data\house-prices\processed(py)\elasticnet.csv
Decision Tree#
def train_tree(X_train, y_train):
# Define the Decision Tree Regressor
tree = DecisionTreeRegressor(random_state=42)
# Set up hyperparameter grid for tuning
param_grid = {
'max_depth': [3, 5, 7, 10, 15, None],
'min_samples_split': [2, 5, 10, 20, 50],
'min_samples_leaf': [1, 2, 5, 10, 20]
}
# Use GridSearchCV to find the best hyperparameters
grid_search = GridSearchCV(
estimator=tree,
param_grid=param_grid,
scoring='neg_root_mean_squared_error', # Minimize RMSE
cv=5, # 5-fold cross-validation
verbose=1,
n_jobs=-1 # Use all available cores
)
# Fit the grid search to the training data
grid_search.fit(X_train, y_train)
# Print the best parameters and RMSE
print("Best parameters:", grid_search.best_params_)
print("Best RMSE:", -grid_search.best_score_)
# Use the best model to predict on the test set
return grid_search.best_estimator_
tree_model = train_tree(X_train_split, y_train_split)
Fitting 5 folds for each of 150 candidates, totalling 750 fits
Best parameters: {'max_depth': 10, 'min_samples_leaf': 10, 'min_samples_split': 2}
Best RMSE: 0.17498563457387445
C:\Users\ArnoZ\AppData\Roaming\Python\Python312\site-packages\numpy\ma\core.py:2846: RuntimeWarning: invalid value encountered in cast
_data = np.array(data, dtype=dtype, copy=copy,
tree_valid_pred = ridge_model.predict(X_valid_split)
tree_valid_rmse = root_mean_squared_error(y_valid_split, tree_valid_pred)
print(f"Validation RMSE (Tree): {tree_valid_rmse}")
Validation RMSE (Tree): 0.12965845670827755
save_submission(ridge_model, X_test_full, test_ids, 'decision_tree.csv')
Submission file saved to: data\house-prices\processed(py)\decision_tree.csv
Random Forest#
def train_random_forest(X_train, y_train):
# Define the Random Forest Regressor
rf = RandomForestRegressor(random_state=42)
# Set up hyperparameter grid for tuning
param_grid = {
'n_estimators': [100, 200, 500], # Number of trees in the forest
'max_depth': [10, 20, None], # Maximum depth of the tree
'min_samples_split': [2, 5, 10], # Minimum samples required to split an internal node
'min_samples_leaf': [1, 2, 4], # Minimum samples required to be at a leaf node
'max_features': ['sqrt', 'log2'], # Number of features to consider at every split
'bootstrap': [True] # Whether bootstrap sampling is used
}
# Use GridSearchCV to find the best hyperparameters
grid_search = GridSearchCV(
estimator=rf,
param_grid=param_grid,
scoring='neg_root_mean_squared_error', # Minimize RMSE
cv=5, # 5-fold cross-validation
verbose=1,
n_jobs=-1 # Use all available cores
)
# Fit the grid search to the training data
grid_search.fit(X_train, y_train)
# Print the best parameters and RMSE
print("Best parameters:", grid_search.best_params_)
print("Best RMSE:", -grid_search.best_score_)
# Use the best model to predict on the test set
return grid_search.best_estimator_
rf_model = train_random_forest(X_train_split, y_train_split)
Fitting 5 folds for each of 162 candidates, totalling 810 fits
Best parameters: {'bootstrap': True, 'max_depth': None, 'max_features': 'sqrt', 'min_samples_leaf': 1, 'min_samples_split': 2, 'n_estimators': 200}
Best RMSE: 0.1352914997113765
rf_valid_pred = rf_model.predict(X_valid_split)
rf_valid_rmse = root_mean_squared_error(y_valid_split, rf_valid_pred)
print(f"Validation RMSE (Random Forest): {rf_valid_rmse}")
Validation RMSE (Random Forest): 0.1484356652188091
save_submission(rf_model, X_test_full, test_ids, 'random_forest.csv')
Submission file saved to: data\house-prices\processed(py)\random_forest.csv
Bagging#
def train_bagging(X_train, y_train):
# Define the base estimator (weak learner)
base_estimator = DecisionTreeRegressor(random_state=42)
# Define the Bagging Regressor
bagging_model = BaggingRegressor(
estimator=base_estimator, # Updated parameter name
random_state=42
)
# Set up hyperparameter grid for tuning
param_grid = {
'n_estimators': [10, 50, 100, 200], # Number of base estimators
'max_samples': [0.5, 0.7, 1.0], # Fraction of samples to draw
'max_features': [0.5, 0.7, 1.0], # Fraction of features to draw
'estimator__max_depth': [3, 5, 10, None] # Depth of decision trees
}
# Use GridSearchCV to find the best hyperparameters
grid_search = GridSearchCV(
estimator=bagging_model,
param_grid=param_grid,
scoring='neg_root_mean_squared_error', # Minimize RMSE
cv=5, # 5-fold cross-validation
verbose=1,
n_jobs=-1 # Use all available cores
)
# Fit the grid search to the training data
grid_search.fit(X_train, y_train)
# Print the best parameters and RMSE
print("Best parameters:", grid_search.best_params_)
print("Best RMSE:", -grid_search.best_score_)
# Use the best model to predict on the test set
return grid_search.best_estimator_
bag_model = train_bagging(X_train_split, y_train_split)
Fitting 5 folds for each of 144 candidates, totalling 720 fits
Best parameters: {'estimator__max_depth': None, 'max_features': 0.5, 'max_samples': 1.0, 'n_estimators': 200}
Best RMSE: 0.13509426431781696
bag_valid_pred = bag_model.predict(X_valid_split)
bag_valid_rmse = root_mean_squared_error(y_valid_split, bag_valid_pred)
print(f"Validation RMSE (Bagging): {bag_valid_rmse}")
Validation RMSE (Bagging): 0.14377696858693548
save_submission(bag_model, X_test_full, test_ids, 'bagging.csv')
Submission file saved to: data\house-prices\processed(py)\bagging.csv
XGBoost#
def train_xgb(X_train, y_train):
# Convert to DMatrix for GPU compatibility
dtrain = DMatrix(X_train, label=y_train)
# Define the XGBoost Regressor
xgb = XGBRegressor(
objective='reg:squarederror', # Regression objective
random_state=42,
tree_method = "hist",
device = "cuda", # enable gpu
n_jobs=-1 # Use all available cores
)
# Set up hyperparameter grid for tuning
param_grid = {
'n_estimators': [100, 300], # Number of boosting rounds
'learning_rate': [0.05, 0.1, 0.2], # Step size shrinkage
'max_depth': [3, 5, 7], # Maximum tree depth
'subsample': [0.8, 1.0], # Fraction of samples used for training each tree
'colsample_bytree': [0.8, 1.0], # Fraction of features used for training each tree
'gamma': [0, 0.1, 0.2, 0.3], # Minimum loss reduction required to split
'reg_alpha': [0, 0.1, 1, 10], # L1 regularization
'reg_lambda': [0, 0.1, 1, 10], # L2 regularization
'min_child_weight': [1, 3, 5, 10] # Minimum child weight
}
# Use GridSearchCV to find the best hyperparameters
grid_search = RandomizedSearchCV(
estimator=xgb,
param_distributions=param_grid,
n_iter=100,
scoring='neg_root_mean_squared_error', # minimize RMSE
cv=5, # 5-fold cross-validation
verbose=1,
n_jobs=-1 # use all available cores
)
# Fit the grid search to the training data
grid_search.fit(X_train, y_train)
# Print the best parameters and RMSE
print("Best parameters:", grid_search.best_params_)
print("Best RMSE:", -grid_search.best_score_)
# Use the best model to predict on the test set
return grid_search.best_estimator_
xgb_model = train_xgb(X_train_split, y_train_split)
Fitting 5 folds for each of 100 candidates, totalling 500 fits
Best parameters: {'subsample': 0.8, 'reg_lambda': 0.1, 'reg_alpha': 0, 'n_estimators': 300, 'min_child_weight': 10, 'max_depth': 5, 'learning_rate': 0.05, 'gamma': 0, 'colsample_bytree': 0.8}
Best RMSE: 0.12320914496713031
xgb_valid_pred = xgb_model.predict(X_valid_split)
xgb_valid_rmse = root_mean_squared_error(y_valid_split, xgb_valid_pred)
print(f"Validation RMSE (XGBoost): {xgb_valid_rmse}")
Validation RMSE (XGBoost): 0.14073594419026517
C:\Users\ArnoZ\AppData\Roaming\Python\Python312\site-packages\xgboost\core.py:158: UserWarning: [00:10:02] WARNING: C:\buildkite-agent\builds\buildkite-windows-cpu-autoscaling-group-i-0c55ff5f71b100e98-1\xgboost\xgboost-ci-windows\src\common\error_msg.cc:58: Falling back to prediction using DMatrix due to mismatched devices. This might lead to higher memory usage and slower performance. XGBoost is running on: cuda:0, while the input data is on: cpu.
Potential solutions:
- Use a data structure that matches the device ordinal in the booster.
- Set the device for booster before call to inplace_predict.
This warning will only be shown once.
warnings.warn(smsg, UserWarning)
save_submission(xgb_model, X_test_full, test_ids, 'xgboost.csv')
Submission file saved to: data\house-prices\processed(py)\xgboost.csv
References#
Kaggle Competition: https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques/overview
Dataset Description: https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques/data
